Discrete Fourier Transform (DFT)#
ใน tutorial ที่แล้ว เราได้เรียนรู้ว่าเราสามารถศึกษา continuous-time signal \(x_c(t)\) ในทางปฏิบัติได้ ผ่านการเก็บข้อมูลมาแค่บางส่วน (sampling) ถ้าหากเรามี sampling rate ที่สูงพอ ข้อมูล discrete-time signal หรือ \(x[n]=x_c(nT)\) ที่เราเก็บมาจะมีข้อมูลของ \(x_c(t)\) อย่างครบถ้วน ทำให้เราสามารถทำการวิเคราะห์ \(x[n]\) แทน \(x_c(t)\) โดยที่ใช้ทรัพยากรการคำนวณที่มีอยู่อย่างจำกัดได้
Convolution#
ก่อนที่เราจะเริ่มเรียนรู้เกี่ยวกับ Discrete Fourier Transform (DFT) เราจะมาเรียนรู้เกี่ยวกับ Convolution กันก่อนผ่าน video lecture นี้
Discrete Fourier Transform (DFT)#
ในการศึกษา signal ใด ๆ หนึ่งในวิธีที่ได้รับความนิยมมาก คือ การดูว่า signal นั้นเกิดจากการเอา signal มีคลื่นความถี่เท่าไหร่มาผสมกันบ้าง ผ่านการใช้ Discrete Fourier Transform (DFT)
Slides: Discrete Fourier Transform (DFT)
กำหนดให้เรามี discrete-time signal \(x[n]\) เราสามารถใช้ DFT แปลง \(x[n]\) จาก time domain ให้อยู่ใน frequency domain ได้ โดยเราจะเรียก signal ที่ถูกแปลงค่าว่า \(X[k]\) ซึ่งผลลัพธ์ที่ได้ จะมีโอกาสมีค่าเป็นจำนวนเชิงซ้อน หรือจำนวนจริง ก็ได้
หาก \(X[k]\) มีค่าไม่เท่ากับศูนย์ แปลว่า time signal ที่เรากำลังวิเคราะห์อยู่มี signal ที่มีคลื่นความถี่นั้นเป็นส่วนประกอบ
ใน scipy เราสามารถคำนวณ DFT ของ signal ใด ๆ ด้วย Fast Fourier Transform (FFT) algorithm ผ่านการเรียกใช้ฟังก์ชัน fft ตามตัวอย่างด้านล่าง
หมายเหตุ
Fast Fourier Transform (FFT) เป็นเทคนิคที่ถูกพัฒนามาเพื่อคำนวณ DFT ได้อย่างรวดเร็ว
ถึงแม้ว่าใน Brain Code Camp เราจะใช้ FFT ในการแปลง signal จาก time domain ไปสู่ frequency domain แต่จริง ๆ แล้ว FFT สามารถใช้ในการแปลง signal จาก domain ตั้งต้นอะไรก็ได้ เช่น ในกรณีของรูปภาพ (2D signal) ซึ่งเราจะเรียกว่าอยู่ใน spatial domain (หรือ image-domain) ก็สามารถถูกแปลงไปสู่ spatial frequency domain ได้ผ่านการใช้ FFT
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq, ifft, ifftshift
import math
เตรียมฟังก์ชันไว้สำหรับใช้คำนวณ DFT (ผ่านการใช้ fft ของ scipy) และแสดงผลลัพธ์ที่เกิดขึ้น
# ฟังก์ชันสำหรับสร้าง time signal ซึ่งเป็นฟังก์ชัน sine ที่มีความถี่ 'freq', มี sampling rate คือ 'f_s' และมีระยะเวลาในแกนเวลาเท่ากับ 'duration'
def generate_sine_wave(freq, f_s, duration):
# คำนวณค่า sampling period (ระยะห่างระหว่างจุดที่เก็บมาสองจุดในแกนเวลา)
T = 1/f_s
# คำนวณจำนวนจุดที่มีใน signal
num_points = math.floor(f_s*duration)
# สร้างแกนเวลา
t = np.linspace(0.0, num_points*T, num_points, endpoint=False)
# สร้าง signal x(t) = sin(2*pi*freq*t)
x = np.sin(2*np.pi*freq*t)
return x, t
def compute_DFT(x_sampled, f_s):
# คำนวณจำนวนจุดที่มีใน signal
num_points = x_sampled.shape[0]
# ใช้ FFT ในการแปลงข้อมูลจาก time domain ไปเป็น frequency domain
X_fft = fft(x_sampled)
# สร้างแกนความถี่ (frequency)
freq = np.fft.fftfreq(num_points, d=1/f_s)
return X_fft, freq
def plot_discrete_time_freq_signal(x_sampled, X_fft, freq):
fig, ax = plt.subplots(3, 1, figsize=(15, 12))
fig.tight_layout(pad=5.0)
# โดยปกติแล้วเวลาเรากราฟ discrete-time signal เราจะใช้ n แทนที่จะใช้เวลาจริงในแกน x
ax[0].scatter(range(x_sampled.shape[0]), x_sampled, c='b')
ax[0].plot(range(x_sampled.shape[0]), x_sampled, c='b', alpha=0.4) # plot เส้นลากผ่านจุดที่เก็บมา เพื่อให้เห็นหน้าตาของข้อมูลโดยคร่าว ๆ
ax[0].set(xlabel='n', ylabel='x[n]')
ax[0].set_title(f"Discrete time signal x[n] sampled from " + r"$x_c(t)$")
ax[0].grid(True)
# Plot magnitude ของ X[k]
ax[1].scatter(freq, np.abs(X_fft), c='b')
ax[1].plot(freq, np.abs(X_fft), 'b', alpha=0.4)
ax[1].set(xlabel='Frequency (Hz)', ylabel='|X[k]|')
ax[1].set_title(f"X[k], DFT of x[n]")
ax[1].set_xticks(np.arange(np.min(freq), np.max(freq), 10))
ax[1].set_xticklabels(ax[1].get_xticks(), rotation = 70)
ax[1].grid(True)
# Plot phase ของ X[k]
ax[2].scatter(freq, np.unwrap(np.angle(X_fft)), c='b')
ax[2].plot(freq, np.unwrap(np.angle(X_fft)), 'b', alpha=0.4)
ax[2].set(xlabel='Frequency (Hz)', ylabel='Phase of X[k]')
ax[2].set_title(f"X[k], DFT of x[n]")
ax[2].set_xticks(np.arange(np.min(freq), np.max(freq), 10))
ax[2].set_xticklabels(ax[2].get_xticks(), rotation = 70)
ax[2].grid(True)
plt.show()
ตัวอย่างที่ 1#
ทดลองกับกรณีที่ signal เป็นฟังก์ชัน sine ที่มีค่าความถี่เดียว
freq_sine = 20 # ค่าความถี่ของฟังก์ชัน sine (Hz)
f_s = 500 # อัตราการเก็บข้อมูล หรือ sampling rate (samples/s หรือ Hz)
duration = 0.5 # ระยะเวลาของ signal (s)
# สร้าง time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่ 'freq_sine' Hz ที่มีค่า sampling rate อยู่ที่ 'f_s' แสดงถึง discrete-time signal ที่เก็บมา
x_sampled, t_sampled = generate_sine_wave(freq=freq_sine, f_s=f_s, duration=duration)
# คำนวณ DFT ของ x[n] และ แกน freq สำหรับใช้ plot
X_fft, freq = compute_DFT(x_sampled, f_s)
# Plot ผลที่ได้
plot_discrete_time_freq_signal(x_sampled, X_fft, freq)
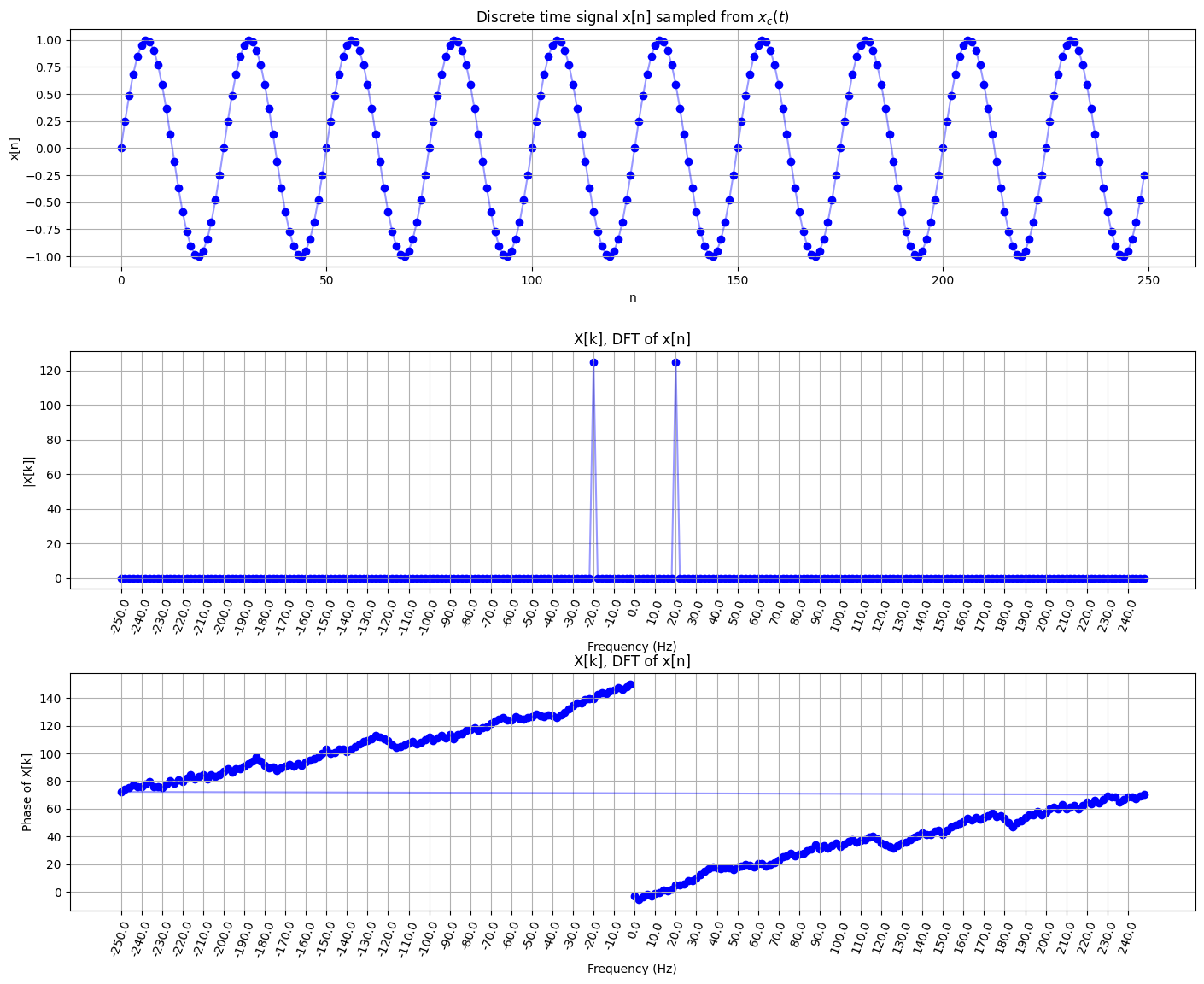
จะเห็นได้ว่า DFT ของ signal ด้านบน \(X[k]\) มี peak อยู่ที่ 20 Hz (และ -20 Hz) พอดี โดยที่ไม่มีความถี่อื่น ๆ เลย สอดคล้องกับ \(x[n]\) ซึ่งเป็นฟังก์ชัน sine ที่ความถี่ 20 Hz
หมายเหตุ โดยปกติแล้ว หากเราใช้ sampling rate ที่มีค่าเป็น \(f_s\) เรามักจะแสดงผลของ DFT โดยกำหนดให้แกน frequency มีค่าความถี่น้อยสุดอยู่ที่ \(-f_s\) และค่าความถี่มากสุดอยู่ที่ \(f_s\)
ตัวอย่างที่ 2#
ต่อไปเรามาลองทดสอบดู signal \(x[n]\) ที่มีค่าความถี่มากกว่า 1 ค่า เช่น
\(x[n]\) คือ signal ที่ถูกเก็บข้อมูลมาจาก \(x_c(t)= \sin (2π \times 20t) + 0.5 \sin (2π \times 50t)\)
# กำหนดค่า sampling rate
f_s = 500
# สร้าง discrete time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่ 20 Hz
x_sampled_20Hz, t_sampled = generate_sine_wave(freq=20, f_s=f_s, duration=duration)
# สร้าง discrete time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่ 50 Hz
x_sampled_50Hz, t_sampled = generate_sine_wave(freq=50, f_s=f_s, duration=duration)
# สร้าง signal ที่เกิดจากการนำเอา signal ด้านบนทั้งสองตัวมาบวกกัน โดย signal ที่มีความถี่ 50 Hz จะถูกลด amplitude มาครึ่งหนึ่ง
x_combined = x_sampled_20Hz + 0.5*x_sampled_50Hz
# คำนวณ DFT ของ signal นี้
X_fft, freq = compute_DFT(x_combined, f_s)
# แสดงผล
plot_discrete_time_freq_signal(x_combined, X_fft, freq)
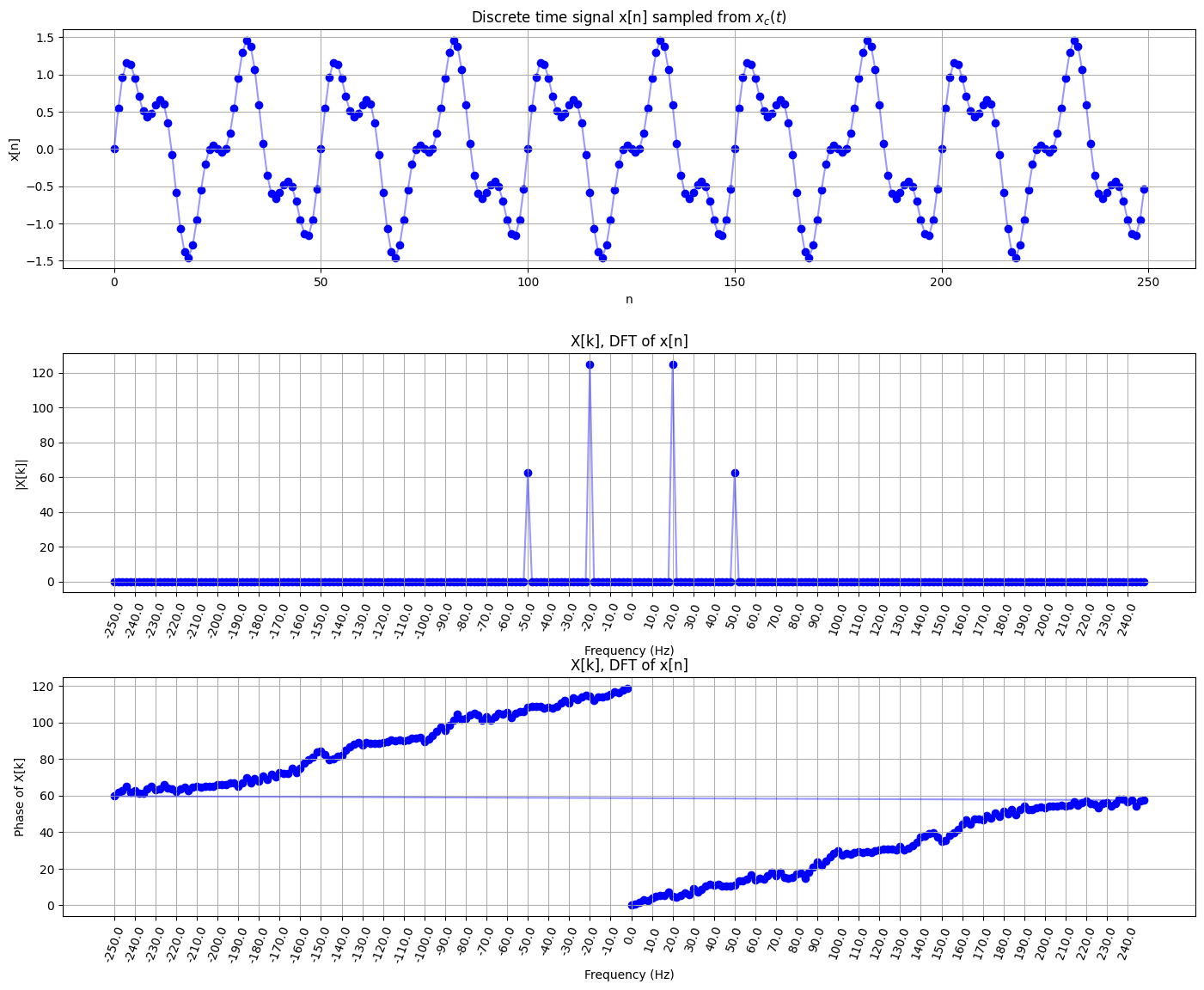
จากกราฟด้านบนจะเห็นได้ว่า DFT ของ signal มีคุณสมบัติที่สอดคล้องกับคุณสมบัติของ \(x[n]\) ซึ่งเป็น signal ที่ถูกเก็บข้อมูลมาจาก \(x_c(t)= \sin (2π \times 20t) + 0.5 \sin(2π \times 50t)\) ดังนี้
มี peak อยู่ที่ \(\pm 20\) Hz และ \(\pm 50\) Hz
peak ที่ความถี่ \(\pm 50\) Hz มีความสูงแค่ครึ่งเดียวของ peak ที่ความถี่ \(\pm 20\) Hz
ถ้าหากเรามอง signal ใน time domain เราก็อาจจะบอกได้ยากว่า signal นี้เกิดจากการนำเอา signal ที่มีความถี่เท่าไหร่ มารวมกันบ้าง โดยเฉพาะในกรณีที่ signal เราซับซ้อนมาก ๆ ซึ่ง DFT ก็เป็นหนึ่งในเทคนิคที่จะมาช่วยเราดูข้อมูลในส่วนนี้ได้
Simple Filtering#
สมมติว่าเราสืบทราบมาว่า signal จากตัวอย่างด้านบน มีที่มาจากสัญญาณสมองที่มีความถี่ไม่เกิน 30 Hz เท่านั้น แต่พอเรามาวิเคราะห์ใน frequency domain เรากลับเจอความถี่ที่ 20 Hz และ 50 Hz
ในการเก็บข้อมูลทาง biomedical เรามักจะพบเจอสัญญาณรบกวนที่เรียกว่า Powerline noise ซึ่งเป็นสัญญาณที่มักมีค่าหลักอยู่ที่ 50 Hz และ 60 Hz (และ harmonics ของมัน) ขึ้นอยู่กับสถานที่ที่เราเก็บข้อมูล
เนื่องจากสถานการณ์นี้กำหนดให้เราสนใจสัญญาณสมองที่มีความถี่ไม่เกิน 30 Hz เท่านั้น และ เราพบว่ามีสัญญาณแปลก ๆ ที่ค่า 50 Hz ซึ่งคาดการณ์ว่าจะเป็น powerline noise ทำให้เวลาเราจะนำเอา signal นี้ไปวิเคราะห์หรือประมวลผลต่อ เราควรกำจัดสัญญาณรบกวนที่เราเจอที่ 50 Hz ทิ้งไป
เรามาลองลบสัญญาณที่ 50 Hz นี้ โดยการ
แปลงข้อมูลให้ไปอยู่ใน frequency domain โดยการใช้
fft(\(X[k] = \text{FFT}\{x[n]\}\))สร้างฟังก์ชัน \(W[k]\) ที่มีค่าเป็น 0 ตรงค่าความถี่ที่เราต้องการกำจัด และมีค่าเป็น 1 ตรงค่าความถี่ที่เราต้องการเก็บไว้ ในที่นี่เราจะเรียก \(W\) ว่าเป็น window หรือ filter
คำนวนผลลัพธ์โดยการใช้สมการ \(X_\text{filtered}[k] = X[k] \times W[k]\) สำหรับทุกค่า \(k\) เพื่อลบ peak ของ \(X[k]\) ที่ \(\pm 50\) Hz ออกใน frequency domain (ในทางเทคนิค จะเรียกว่า filter ข้อมูลที่ \(\pm 50\) Hz ทิ้งไป)
แปลง \(X_\text{filtered}[k]\) ซึ่งเป็นข้อมูลที่ถูก filter แล้วใน frequency domain กลับมาสู่ time domain โดยการคำนวณ Inverse Discrete Fourier Transform (IDFT) ผ่านการเรียกใช้
ifftของscipy
def compute_and_plot_filtered_signal(x_sampled, f_s):
# Step 1: ใช้ DFT ในการแปลงข้อมูลเข้าสู่ frequency domain
X_fft, freq = compute_DFT(x_sampled, f_s)
# Step 2: สร้าง Window function ใน frequency domain, W[k] โดยในที่นี้จะลองสร้างเป็น window สำหรับ ลบข้อมูลความถี่ที่มีค่ามากกว่า 30 Hz หรือความถี่น้อยกว่า -30 Hz
W_fft = np.ones_like(X_fft)
W_fft[(freq < -30) | (freq > 30)] = 0
# Step 3: คำนวณ X[k]*W[k] สำหรับทุกค่า k
X_fft_filtered = X_fft * W_fft
# Step 4: แปลงค่า X_fft_filtered กลับมาสู่ time domain เพื่อดูผล
x_filtered = ifft(X_fft_filtered)
# ลองแปลงค่า W กลับมาสู่ time domain เช่นกัน
w = ifftshift(ifft(W_fft))
# Plot signal ก่อนและหลังการ filter
fig, ax = plt.subplots(3, 2, figsize=(18, 12))
fig.tight_layout(pad=5.0)
# Plot x[n]
ax[0, 0].scatter(range(x_sampled.shape[0]), x_sampled, c='b')
ax[0, 0].plot(range(x_sampled.shape[0]), x_sampled, c='b', alpha=0.4) # plot เส้นลากผ่านจุดที่เก็บมา เพื่อให้เห็นหน้าตาของข้อมูลโดยคร่าว ๆ
ax[0, 0].set(xlabel='n', ylabel='x[n]')
ax[0, 0].set_title(f"Discrete time signal x[n] sampled from " + r"$x_c(t)$")
ax[0, 0].grid(True)
# Plot w[n]
ax[1, 0].scatter(range(w.shape[0]), np.real(w), c='b')
ax[1, 0].plot(range(w.shape[0]), np.real(w), c='b', alpha=0.4) # plot เส้นลากผ่านจุดที่เก็บมา เพื่อให้เห็นหน้าตาของข้อมูลโดยคร่าว ๆ
ax[1, 0].set(xlabel='n', ylabel='w[n]')
ax[1, 0].set_title(f"Window function to be used for filtering")
ax[1, 0].grid(True)
# Plot x_filtered[n]
ax[2, 0].scatter(range(x_filtered.shape[0]), np.real(x_filtered), c='b')
ax[2, 0].plot(range(x_filtered.shape[0]), np.real(x_filtered), c='b', alpha=0.4) # plot เส้นลากผ่านจุดที่เก็บมา เพื่อให้เห็นหน้าตาของข้อมูลโดยคร่าว ๆ
ax[2, 0].set(xlabel='n', ylabel='Filtered x[n]')
ax[2, 0].set_title(f"Filtered x[n]")
ax[2, 0].grid(True)
# Plot X[k]
ax[0, 1].scatter(freq, np.abs(X_fft), c='b')
ax[0, 1].plot(freq, np.abs(X_fft), 'b', alpha=0.4)
ax[0, 1].set(xlabel='Frequency (Hz)', ylabel='|X[k]|')
ax[0, 1].set_title(f"X[k], DFT of x[n]")
ax[0, 1].set_xticks(np.arange(np.min(freq), np.max(freq), 20))
ax[0, 1].set_xticklabels(ax[0, 1].get_xticks(), rotation=70)
ax[0, 1].grid(True)
# Plot W[k]
ax[1, 1].scatter(freq, np.abs(W_fft), c='b')
ax[1, 1].plot(freq, np.abs(W_fft), 'b', alpha=0.4)
ax[1, 1].set(xlabel='Frequency (Hz)', ylabel='|W[k]|')
ax[1, 1].set_title(f"W[k], DFT of w[n]")
ax[1, 1].set_xticks(np.arange(np.min(freq), np.max(freq), 20))
ax[1, 1].set_xticklabels(ax[1, 1].get_xticks(), rotation=70)
ax[1, 1].grid(True)
# Plot X_filtered[k]
ax[2, 1].scatter(freq, np.abs(X_fft_filtered), c='b')
ax[2, 1].plot(freq, np.abs(X_fft_filtered), 'b', alpha=0.4)
ax[2, 1].set(xlabel='Frequency (Hz)', ylabel='|Filtered X[k]|')
ax[2, 1].set_title(f"Filtered X[k]")
ax[2, 1].set_xticks(np.arange(np.min(freq), np.max(freq), 20))
ax[2, 1].set_xticklabels(ax[2, 1].get_xticks(), rotation=70)
ax[2, 1].grid(True)
plt.show()
compute_and_plot_filtered_signal(x_combined, f_s)
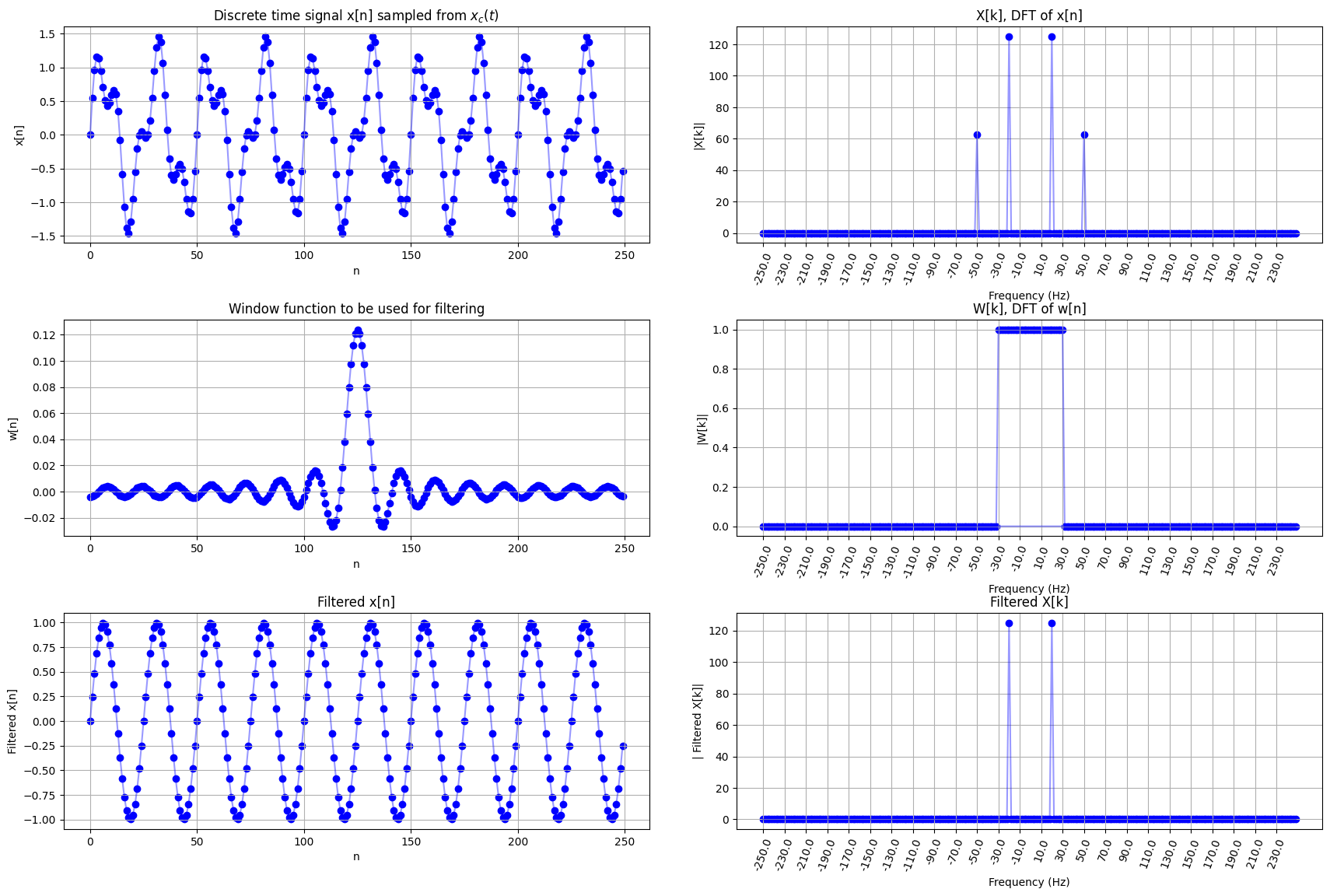
จากการสำรวจผลทั้งใน time domain (ภาพซ้ายล่าง) และใน frequency domain (ภาพขวาล่าง) พบว่าข้อมูลค่าความถี่ \(\pm 50\) Hz ซึ่งเราสันนิษฐานว่าเป็นสัญญาณรบกวน ได้ถูกกำจัดออกไป
ในตัวอย่างนี้เราใช้ \(W[k]\) ที่มีค่าเป็น 0 ในบริเวณค่าความถี่ที่เราต้องการกำจัด และมีค่าเป็น 1 ในบริเวณค่าความถี่ที่เหลือ ฟังก์ชัน window ที่มีลักษณะแบบนี้มีชื่อเรียกว่า rectangular window เนื่องจากเป็น window ที่มีหน้าตาเหมือนสีเหลี่ยมผืนผ้า (rectangle) นั่นเอง
หากได้มีโอกาสศึกษาเพิ่มเติมจะทราบว่า rectangular window มีข้อจำกัดหลายอย่าง ซึ่งในสถานการณ์จริง มี window อีกหลากหลายประเภทให้เลือกใช้ เช่น Hamming window, Hanning window, Kaiser ฯลฯ (สามารถดูตัวอย่าง window ได้จาก scipy.signal.windows) การเลือกใช้ window ก็ขึ้นอยู่กับสถานการณ์การทำงานของเรา
DFT properties#
ในตอนนี้เราจะมาดู video lecture เกี่ยวกับคุณสมบัติบางอันที่สำคัญของ DFT ที่เราจะใช้ในการทำความเข้าใจ tutorial ต่อไปกัน
Sampling and Aliasing#
(Optional)
สุดท้ายนี้เราสามารถทำความเข้าใจเพิ่มเติมเกี่ยวกับที่มาว่าทำไมเราต้องเลือก sampling rate ที่มีค่าสูงเกินค่าบางค่า โดยจะเราจะดูพฤติกรรมของ signal ของเราทั้งใน time domain และ frequency domain เมื่อเราเปลี่ยนค่า sampling rate กัน
ผู้จัดเตรียม code ใน tutorial: ดร. อิทธิ ฉัตรนันทเวช