Sampling and Signal Averaging#
ใน module นี้ เราจะมาเรียนรู้เกี่ยวกับการประมวลผลสัญญาณ (signal processing) แบบพื้นฐานที่มีโอกาสพบเจอบ่อย ๆ ในการประมวลผลและวิเคราะห์ข้อมูลทาง neuroscience เช่น electroencephalogram (EEG) โดยจะเน้นการเรียนรู้ผ่าน SciPy
หมายเหตุ ใน module นี้ เราจะใช้คำว่า signal แทนคำว่า สัญญาณ
Sampling#
import numpy as np
from numpy.random import normal
import matplotlib.pyplot as plt
import math
import ipywidgets as widgets # ใช้สำหรับการทำ interactive display
np.random.seed(42)
กำหนดให้ \(x\) เป็น signal ที่มีค่าเปลี่ยนไปขึ้นอยู่กับแกนเวลา (continuous-time signal) และ กำหนดให้ \(x_c(t)\) คือค่าของ signal นั้นที่เวลา \(t\)
ในการเก็บข้อมูลจริง เราไม่สามารถเก็บค่าของ signal นี้ในทุก ๆ ช่วงเวลา \(t\) ได้ เนื่องจากข้อจำกัดทางด้านทรัพยากร เราจึงพึ่งพาการเก็บตัวอย่าง signal นี้แค่บางส่วน (เรียกว่า กระบวนการ sampling)
วิธีที่ตรงไปตรงมาที่สุดที่สำหรับการเก็บตัวอย่างก็คือการเก็บค่าของ \(x_c\) ที่มีระยะห่างในแกนเวลาเท่า ๆ กัน ยกตัวอย่าง เช่น ถ้าเราเริ่มเก็บค่าของ \(x_c\) ที่เวลา \(t=0\) และเราเก็บค่าทุก ๆ \(0.025\) วินาที (sampling period \(T = 0.025 \ s\)) เราจะได้ค่าของ signal \(x_c\) ที่ประกอบด้วย \(x_c(0), \ x_c(0.025), \ x_c(0.050), \ x_c(0.075), \ x_c(0.010), \ ...\)
อัตราการเก็บข้อมูล (เช่น จำนวนจุดที่เก็บมาต่อวินาที) มีชื่อเรียกทางเทคนิคว่า sampling rate หรือ sampling frequency \(f_s\) ซึ่งคำนวณได้จาก
หากเรากำหนด sampling rate \(f_s\) เป็น \(\frac{1}{T}\) Hz แปลว่า ทุก ๆ \(T\) วินาที เราจะเก็บข้อมูลมา 1 จุด
ข้อมูลที่เราเก็บมาจะประกอบด้วยค่า \(x_c(0), \ x_c(T), \ x_c(2T), \ x_c(3T), \ ..., \ x_c(nT)\) ตามภาพประกอบด้านล่าง
วิธีหนึ่งที่เป็นที่นิยมในการเรียกค่าที่เก็บมาไม่ให้ดูยุ่งเหยิงจนเกินไปก็คือการเขียนแบบไม่ต้องมีค่า \(T\) เช่น
เขียน \(x[0]\) แทน \(x_c(0*T)\)
เขียน \(x[1]\) แทน \(x_c(1*T)\)
เขียน \(x[2]\) แทน \(x_c(2*T)\)
เขียน \(x[3]\) แทน \(x_c(3*T)\)
สรุปเป็นสมการได้เป็น \(x[n]=x_c(nT)\)
ตัวอย่างด้านล่างแสดง continous-time signal \(x_c(t)=sin(2π \times 20t)\) ด้วยสีน้ำเงิน และ จุดข้อมูลที่เก็บมา (discrete-time signal) \(x[n]\) ด้วยสีแดง
# ฟังก์ชันสำหรับสร้าง time signal ซึ่งเป็นฟังก์ชัน sine ที่มีความถี่ freq, มี sampling period คือ f_s และมีระยะเวลาในแกนเวลาเท่ากับ duration
def generate_sine_wave(freq, f_s, duration):
# คำนวณค่า sampling period (ระยะห่างระหว่างจุดที่เก็บมาสองจุดในแกนเวลา)
T = 1/f_s
# คำนวณจำนวนจุดที่มีใน signal
num_points = math.floor(f_s*duration)
# สร้างแกนเวลา
t = np.linspace(0.0, num_points*T, num_points, endpoint=False)
# สร้าง signal x(t) = sin(2*pi*freq*t)
x = np.sin(2*np.pi*freq*t)
return x, t
freq_sine = 20 # ค่าความถี่ของฟังก์ชัน sine (Hz)
f_s = 1000 # อัตราการเก็บข้อมูล หรือ sampling rate (samples/s หรือ Hz)
duration = 0.5 # ระยะเวลาของ signal (s)
# สร้าง time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่ 'freq_sine' Hz โดยมีค่า sampling rate สูงมาก ๆ เพื่อใช้เป็นตัวแทน continuous time signal
x_cont, t_cont = generate_sine_wave(freq=freq_sine, f_s=2000, duration=duration)
# สร้าง time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่ 'freq_sine' Hz เหมือนกันแต่ มีค่า sampling rate ต่ำลงตามที่เรากำหนด แสดงถึง discrete time signal ที่เก็บมา
x_sampled, t_sampled = generate_sine_wave(freq=freq_sine, f_s=f_s, duration=duration)
# Plot x(t)
plt.figure(figsize=(8, 14))
plt.subplot(3, 1, 1)
plt.plot(t_cont, x_cont, c='b')
plt.grid()
plt.xlabel('Time (s)')
plt.title(r"$x_c(t)=\sin(2 \pi \times $" + f"{freq_sine} t)")
# Plot x[n]
plt.subplot(3, 1, 2)
plt.scatter(t_sampled, x_sampled, c='r')
plt.grid()
plt.xlabel('n')
plt.title(r"$x_c(t)=\sin(2 \pi \times $" + f"{freq_sine} t) sampled with a sampling rate of {f_s} Hz")
# Plot ทั้ง x(t) และ x[n] ทับกัน
plt.subplot(3, 1, 3)
plt.plot(t_cont, x_cont, c='b', label='x_c(t)')
plt.scatter(t_sampled, x_sampled, c='r', label='x[n]')
plt.grid()
plt.xlabel('Time (s)')
plt.title(r"$x_c(t)=\sin(2 \pi \times $" + f"{freq_sine} t) sampled with a sampling rate of {f_s} Hz")
plt.show()
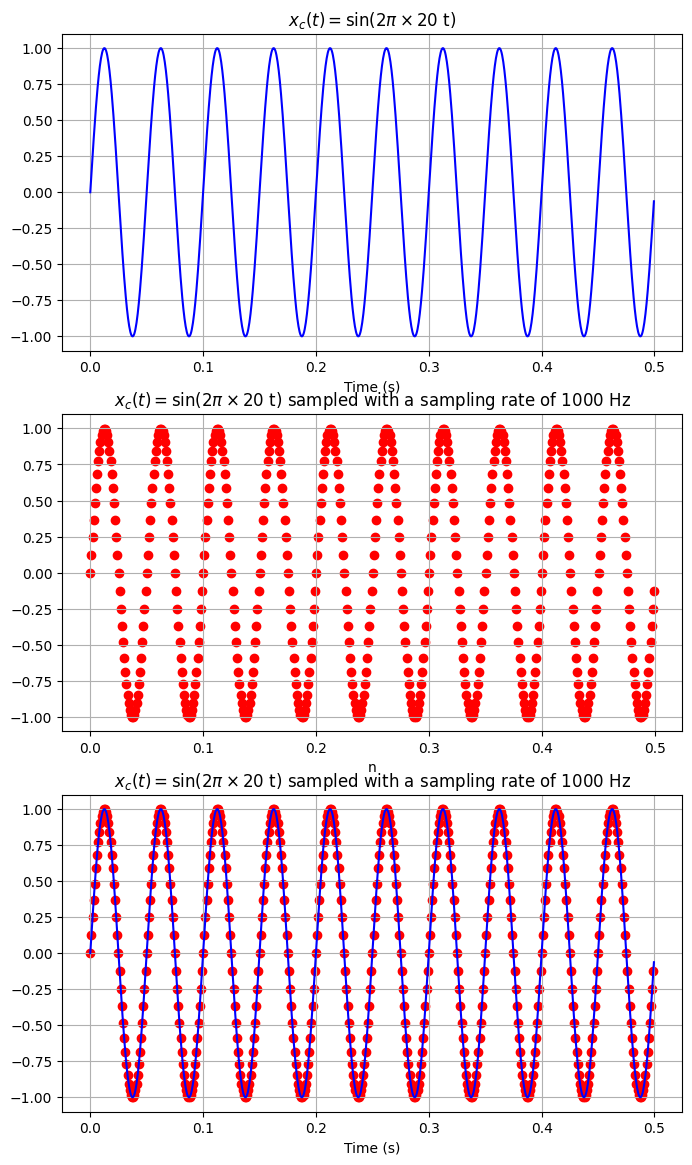
ในตัวอย่างด้านบน เราใช้ sampling rate ที่มีค่าสูง (จุดที่เก็บมีระยะห่างในแกนเวลาน้อย) ทำให้ค่าที่เก็บมา (จุดสีแดง) มีหน้าตาเหมือน continous-time signal (เส้นสีน้ำเงิน) เลย
ด้วยค่า sampling rate ที่สูงเหมือนในกรณีนี้ ต่อให้เราไม่เคยเห็นเส้นสีน้ำเงินเลย เราก็ยังสามารถดูแค่ จุดสีแดง แล้วบอกได้เลยว่า signal นี้คือ sine wave ที่มีความถี่ 20 Hz
หมายเหตุ ถึงแม้ว่าเราจะใช้ scatter ในการแสดง discrete-time signal ในตัวอย่างด้านบน แต่จริง ๆ แล้วในสถานการณ์จริง เราก็จะเห็นการแสดง discrete-time signal ได้ในหลายรูปแบบ ไม่ว่าจะเป็นการใช้ stem หรือใช้ plot ไปเลย
ในตัวอย่างถัดไป เราจะมาลองดูว่าถ้าเราเก็บข้อมูลด้วย sampling rate ที่น้อยลงเรื่อย ๆ (โดยที่ไม่เปลี่ยนค่าอื่น ๆ เช่น ค่า duration = 0.5 s เหมือนเดิม) ข้อมูลที่เราได้รับจะมีหน้าตาเป็นอย่างไร
freq_sine = 20 # ค่าความถี่ของฟังก์ชัน sine (Hz)
f_s = 1000 # อัตราการเก็บข้อมูล หรือ sampling rate (samples/s หรือ Hz)
duration = 0.5 # ระยะเวลาของ signal (s)
# สร้าง time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่ 20 Hz โดยมีค่า sampling rate สูง เพื่อใช้เป็นตัวแทน continuous time signal
x_cont, t_cont = generate_sine_wave(freq=freq_sine, f_s=2000, duration=duration)
f_s_list = [1000, 500, 100, 60, 40, 20] # สร้าง list ที่มีค่า sampling rate ที่ต้องการนำมาทดสอบ
num_sub_figs = len(f_s_list)
plt.figure(figsize=(10,6*num_sub_figs))
for count, f_s in enumerate(f_s_list, start=1):
# สร้าง time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่ 'freq_sine' Hz เหมือนกัน โดยมีค่า sampling rate ที่กำหนดไว้ แสดงถึง discrete time signal ที่เก็บมา
x_sampled, t_sampled = generate_sine_wave(freq=freq_sine, f_s=f_s, duration=duration)
# กราฟทั้ง x(t) และ x[n] ทับกัน
plt.subplot(num_sub_figs, 1, count)
plt.plot(t_cont, x_cont, c='b', label=r"$x_c(t)$")
plt.scatter(t_sampled, x_sampled, c='r', label=r"$x[n]$")
plt.legend()
plt.grid()
plt.xlabel('Time (s)')
plt.title(r"$x_c(t)=\sin(2 \pi \times $" + f"{freq_sine} t) sampled with a sampling rate of {f_s} Hz")
plt.show()
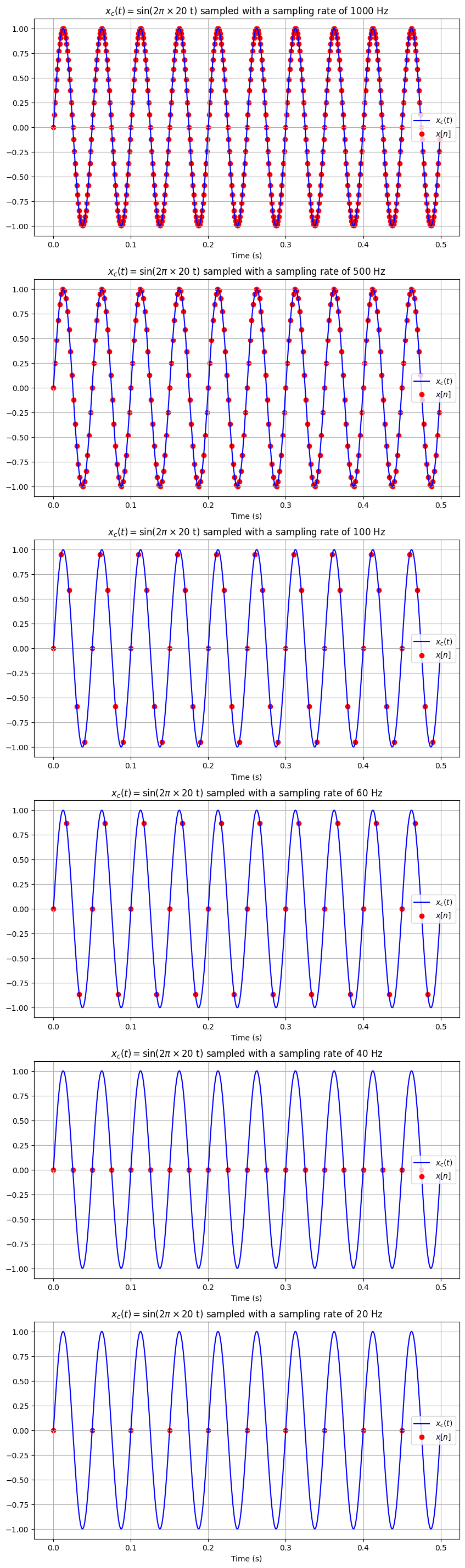
จากตัวอย่างด้านบนจะเห็นได้ว่า ยิ่งมี sampling rate ที่สูง discrete-time signal ที่เราเก็บมา (จุดสีแดง) ก็จะยิ่งมีหน้าตาเหมือนกับ signal จริง (เส้นสีน้ำเงิน) มากขึ้นเรื่อย ๆ แต่สิ่งที่เราต้องแลกมาในการใช้ sampling rate ที่สูงก็คือเราต้องใช้ทรัพยากรในการจัดเก็บข้อมูลมากขึ้น และถ้าหากเราต้องการวิเคราะห์ข้อมูล เราก็จะต้องใช้ทรัพยากรในการประมวลผลที่สูงขึ้นด้วยเช่นกัน
ในทางปฏิบัติ เราเลือก sampling rate ที่มีค่าน้อย (จำนวนจุดสีแดงน้อย) ในขณะที่ยังมากพอที่จะอนุมานหน้าตาของเส้นสีน้ำเงินได้อยู่
หมายเหตุ สำหรับผู้ที่สนใจ เราสามารถใช้ The Nyquist-Shannon sampling theorem ในการช่วยเลือกค่า sampling rate ที่ไม่น้อยจนเกินไปได้ โดยทั่วไปแล้ว เรามักจะเลือก sampling rate \(f_s\) ให้มีค่าที่สูงกว่า 2 เท่าของความถี่ที่เราสนใจ เช่น ถ้าเราต้องการศึกษาสัญญาณจากสมองที่มีชื่อว่าสัญญาณ alpha ซึ่งทางการแพทย์เราทราบว่ามีความถี่อยู่ระหว่าง 8 Hz ถึง 12 Hz เราก็ควรจะเก็บข้อมูลจากสมองที่มีค่า sampling rate อย่างน้อย 24 Hz (ในทางปฏิบัติ เครื่องมือสำหรับใช้วัดสัญญาณจากสมองจะมีค่า sampling rate ตั้งต้นที่สูงกว่านี้มาก ๆ เช่น เกิน 1000 Hz ดังนั้น เราอาจจะไม่ต้องกังวลมากนัก)
ผู้ที่สนใจสามารถรัน code ใน cell ถัดมาได้ เพื่อลองดูผลที่ได้จากการปรับค่า sampling rate โดยที่เราสามารถเปลี่ยนค่าความถี่ของ signal ตั้งต้นเราได้ด้วย
def plot_interactive_fs_example():
@widgets.interact(sampling_rate=widgets.BoundedIntText(1000, min=1, max=1000, description=f"f_s (Hz)"),
freq_wave=widgets.BoundedIntText(10, min=1, max=40, description=f"wave freq"),
show_cont_signal=widgets.Checkbox(True, description='Show continuous time signal'))
def plot_sampled_signal(sampling_rate, freq_wave, show_cont_signal):
duration = 0.5 # ระยะเวลาของ signal (s)
# สร้าง time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่เจาะจง โดยมีค่า sampling rate สูง เพื่อใช้เป็นตัวแทน continuous time signal
x_cont, t_cont = generate_sine_wave(freq=freq_wave, f_s=2000, duration=duration)
# สร้าง time signal ที่เป็นฟังก์ชัน sine ที่มีความถี่เจาะจง เหมือนกันแต่ มีค่า sampling rate ที่น้อยลอง แสดงถึง discrete time signal ที่เก็บมา
x_sampled, t_sampled = generate_sine_wave(freq=freq_wave, f_s=sampling_rate, duration=duration)
# กราฟทั้ง x(t) และ x[n] ทับกัน
plt.figure(figsize=(10, 4))
if show_cont_signal:
plt.plot(t_cont, x_cont, c='b', label=r"$x_c(t)$")
plt.scatter(t_sampled, x_sampled, c='r', label=r"$x[n]$")
plt.legend()
plt.grid()
plt.xlabel('Time (s)')
plt.title(r"$x_c(t)=\sin(2 \pi \times $" + f"{freq_wave} t) sampled with a sampling rate of {sampling_rate} Hz")
plt.ylim(-1.25, 1.25)
plt.show()
plot_interactive_fs_example()
Signal averaging#
ในส่วนนี้ กำหนดให้
มีวัตถุปริศนาที่ปล่อยสัญญาณ \(x_c(t)=sin(2π \times 20t)\) มาตลอดเวลา
เรามีอุปกรณ์วัดข้อมูลชนิดหนึ่งที่เราจะใช้วัดค่าจากวัตถุปริศนานี้ เพียงแต่อุปกรณ์นี้ค่อนข้างเก่ามาก ทำให้เวลาเก็บข้อมูลทีไร จะมีสัญญาณรบกวนเกิดขึ้นอยู่เสมอ กล่าวคือข้อมูลที่เราเก็บมาจะเป็น \(x_c(t)=sin(2π \times 20t) + noise \) เสมอ
สัญญาณรบกวนเป็น Gaussian ที่มีค่าเฉลี่ยเป็น 0 และมีค่า standard deviation คงที่
การเก็บข้อมูลด้วยอุปกรณ์วัดข้อมูลชนิดนี้เสียค่าใช้จ่ายน้อยมาก และ เราสามารถเปิดอุปกรณ์นี้ได้ทั้งวันทั้งคืน
code ด้านล่าง จะเป็น code ที่จำลองการเก็บข้อมูลในแต่ละครั้ง
def collect_one_signal_from_device():
# สัญญาณจริงที่มาจากวัตถุปริศนา
x_true, t_sampled = generate_sine_wave(freq=20, f_s=1000, duration=duration)
# สร้างสัญญาณรบกวน (noise) แบบ Gaussian ที่มีค่าเฉลี่ยอยู่ที่ 0 และค่า standard deviation อยู่ที่ 0.5
noise = normal(0, 0.5, size=x_true.shape)
# สัญญาณที่เครื่องมือวัดของเราเก็บได้
x_sampled_device = x_true + noise
return x_sampled_device, x_true, t_sampled
ลองดู signal ที่เก็บมาได้จากการวัด 1 ครั้ง
# เก็บ signal จากเครื่องนี้มา 1 ครั้ง
x_sampled_device, x_true, t_sampled = collect_one_signal_from_device()
# Plot ข้อมูลออกมาดู
plt.figure()
plt.plot(t_sampled, x_sampled_device, c='r', label='Collected')
plt.plot(t_sampled, x_true, c='b', label='True')
plt.xlabel('Time(s)')
plt.legend()
plt.grid()
plt.show()
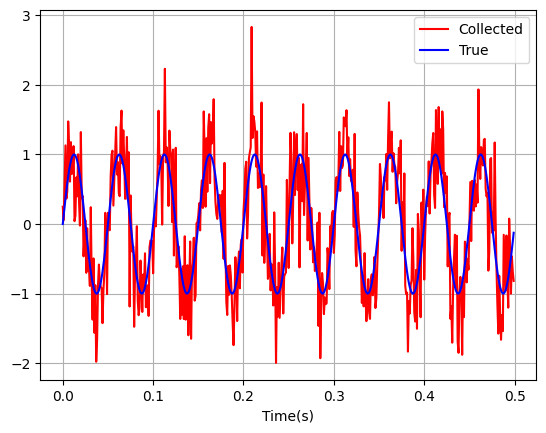
จากตัวอย่างด้านบน จะเห็นว่า signal ที่เราเก็บมาจากอุปกรณ์ของเรา (สีแดง) มีค่าที่ค่อนข้างแตกต่างจากสัญญาณจริง (สีน้ำเงิน) ค่อนข้างมาก เนื่องจากมีสัญญาณรบกวนมาก
วิธีการนึงที่จะช่วยทำให้สัญญาณรบกวนเหล่านี้มีค่าลดลง ก็คือการนำเอา signal ที่เราเก็บมาจากอุปกรณ์ของเราหลาย ๆ รอบ มาลองเฉลี่ยกัน
# จำนวนครั้งที่เก็บข้อมูล
num_collect = 200
# ตัวแปรสำหรับเก็บข้อมูลที่เกิดจากการเอา signal มาบวกกัน
x_sum = np.zeros_like(x_sampled_device)
for count in np.arange(1,num_collect+1):
# เก็บข้อมูลแต่ละครั้ง
x_sampled_device, x_true, t_sampled = collect_one_signal_from_device()
# นำเอา signal ที่เก็บมาได้ในแต่ละครั้งมาบวกกัน
x_sum += x_sampled_device
# แสดงผลเป็นระยะๆ
if count in [5, 10, 15, 20, 25, 200]:
plt.figure()
plt.plot(t_sampled, x_sum/count, c='r', label='Collected')
plt.plot(t_sampled, x_true, c='b', label='True')
plt.xlabel('Time(s)')
plt.title(f"Averaged signal ({count} times)")
plt.legend()
plt.grid()
plt.show()
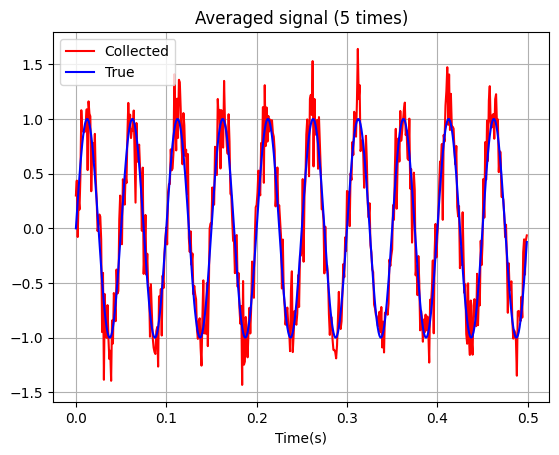
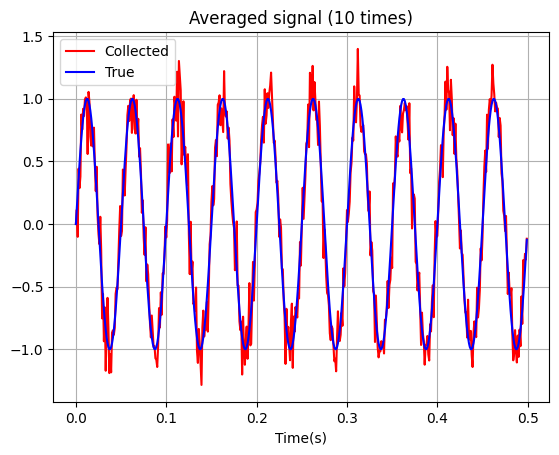
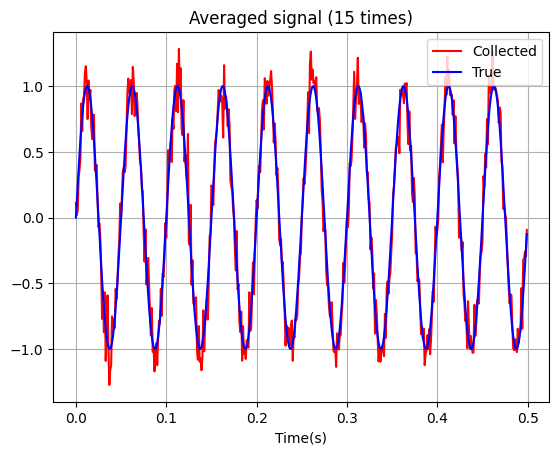
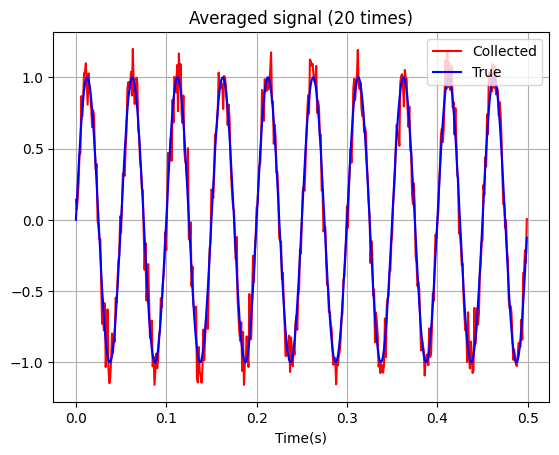
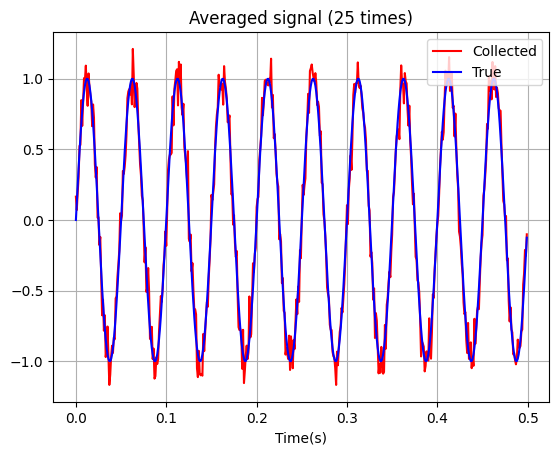
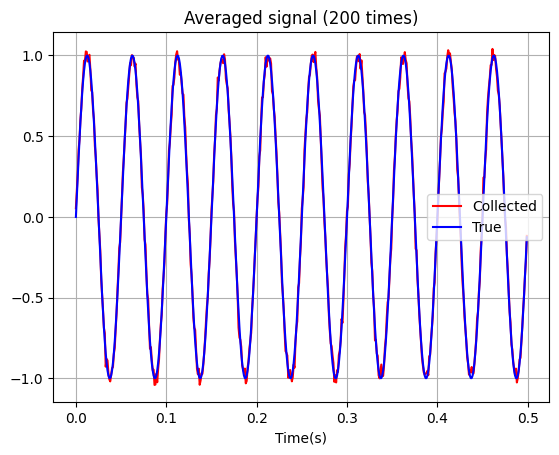
จากตัวอย่างด้านบนจะเห็นได้ว่ายิ่งเราเก็บข้อมูลจากวัตถุปริศนานี้หลาย ๆ รอบด้วยเครื่องมือเดิม และนำเอา signal ที่ได้นั้นมาเฉลี่ย (average) กัน จะพบว่าสัญญาณรบกวนจะค่อย ๆ หายไป ยิ่ง average มากขึ้น ก็จะยิ่งส่งผลให้สัญญาณรบกวนลดลงเรื่อย ๆ
@widgets.interact(n_avgs=widgets.BoundedIntText(1, min=1, max=500, description='# averages'))
def plot_sampled_signal(n_avgs):
# สร้างข้อมูลที่ไม่มีสัญญาณรบกวน (clean signal)
_, x_true, t_sampled = collect_one_signal_from_device()
# ข้อมูลที่เกิดจากการเอา signal มาบวกกัน
x_sum = np.zeros_like(x_true)
for count in np.arange(1, n_avgs+1):
# เก็บข้อมูลแต่ละครั้ง
x_sampled_device, _, _ = collect_one_signal_from_device()
# นำเอา signal ที่เก็บมาได้ในแต่ละครั้งมาบวกกัน
x_sum += x_sampled_device
# แสดงผลที่ average มาแล้ว
plt.figure()
plt.plot(t_sampled, x_sum/count, c='r', label='Collected')
plt.plot(t_sampled, x_true, c='b', label='True')
plt.xlabel('Time(s)')
plt.title(f"Averaged signal ({count} times)")
plt.legend()
plt.grid()
plt.ylim(-3, 3)
plt.show()
ข้อมูลทาง neuroscience หลายประเภท เช่น สัญญาณที่ได้จากเครื่อง electroencephalogram (EEG) เป็น signal ที่มีสัญญาณรบกวนมาก ดังนั้นการทำ signal averaging เป็นการประมวลผลแบบพื้นฐานของข้อมูลเหล่านี้ จึงได้รับความนิยมเป็นอย่างมาก
หมายเหตุ หากเราต้องการวัดคุณภาพของ signal เมื่อเปรียบเทียบกับปริมาณสัญญาณรบกวน ออกมาเป็นตัวเลข (quantitative metric) เราสามารถลอง metric แบบมาตรฐาน เช่น signal-to-noise ratio (SNR) หรือ Contrast-to-noise ratio (CNR) ได้
ผู้จัดเตรียม code ใน tutorial: ดร. อิทธิ ฉัตรนันทเวช