The Basics#
Dimensionality reduction คือ การลดจำนวนมิติของข้อมูล
หากใช้ภาษาทางเทคนิค เราจะเรียกว่าเป็นการแปลงข้อมูลจากข้อมูลใน space ที่มีจำนวนมิติมาก (high-dimensional space) มาสู่ space ที่มีจำนวนมิติน้อย (low-dimensional space) ซึ่งเรามักจะออกแบบการลดจำนวนมิติลง โดยที่สูญเสียข้อมูลน้อยที่สุดเท่าที่ทำได้
ตัวอย่างของข้อมูลที่มีจำนวนมิติมาก
ข้อมูลรูปภาพ gray scale โดยที่แต่ละภาพมีจำนวน pixel เท่ากับ 1,024 x 1,024 = 1,048,576 pixels และเราใช้แต่ละ pixel เป็น feature แปลว่าในกรณีนี้ภาพ 1 ภาพ จะเป็นข้อมูล 1 จุดใน feature space ที่มี 1,048,576 มิติ (1,048,576-dimensional space)
ข้อมูล vdo ที่มีสี (แดง เขียว น้ำเงิน หรือ RGB) โดยเราสามารถมอง vdo เป็นรูปภาพจำนวนมากที่มาเรียงต่อกันได้ ถ้าหากแต่ละภาพใน vdo มี 1,024 x 1,024 pixels และเป็น vdo ความยาว 5 นาที ที่มี frame rate เท่ากับ 24 frame ต่อวินาที ข้อมูลของเราจะเป็นจุดใน space ที่มีทั้งหมด 1,024 x 1,024 x 3 x 24 x 5 x 60 มิติ หรือประมาณ 22 หมื่นล้านมิติ
ข้อมูลสัญญาณสมองที่เก็บมาจากเทคนิค electroencephalogram (EEG) ซึ่งมักจะมี sensor เก็บข้อมูลประมาณ 64 ตัว แต่ละตัวจะเก็บข้อมูลที่ประมาณ 1,000 จุดต่อวินาที ถ้าหากเราเก็บข้อมูลทั้งหมดเป็นเวลา 5 วินาที จะส่งผลให้ข้อมูลของเราอยู่ใน space ที่มีทั้งหมด 64 x 1,000 x 5 = 320,000 มิติ
ถ้าหากเราสามารถลดจำนวนมิติลงได้ จะส่งผลดีอยู่หลายประการ เช่น
เราจะใช้ทรัพยากรการคำนวณน้อยลง เช่น ถ้าหากเราสามารถ represent ภาพ 1 ภาพ ด้วยตัวเลขแค่ 64 ตัว (แทนที่จะ represent ด้วยตัวเลข 1,048,576 ตัว) เราก็จะสามารถนำเอาโมเดลปัญญาประดิษฐ์ที่เรารู้จักมาประมวลผลได้อย่างรวดเร็วและใช้ทรัพยากรการคำนวณน้อย
นอกจากนี้ หากเราลดจำนวนมิติของข้อมูลลงจนเหลือไม่เกิน 3 มิติ ก็จะช่วยให้เราสามารถนำเอาข้อมูลมา plot และดูได้ด้วยตาเปล่า
ในการลดจำนวนมิติของข้อมูล เราสามารถใช้ทั้งเทคนิคที่เป็นแบบ linear หรือ แบบ non-linear ก็ได้ โดยที่แต่ละเทคนิคก็จะมีข้อดีและข้อเสีย และมีสมมติฐานในการใช้งานที่แตกต่างกัน
สมมติว่าเรามีชุดข้อมูลชุดหนึ่ง ที่มีจุดข้อมูลอยู่ทั้งหมด 100 จุด แต่ละจุดข้อมูล \((x,y)\) เป็นข้อมูลใน space ที่มี 2 มิติ (ค่า \(x\) เป็นมิติแรก และค่า \(y\) เป็นมิติที่สอง) และในชุดข้อมูลนี้มีจุดอยู่ 2 ประเภท (2 classes)
class 1: \(y = 1\) โดยที่ \( -4 ≤ x < 0 \)
class 2: \(y = 1\) โดยที่ \( 0 < x ≤ 4 \)
ดังแสดงด้านล่าง
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from matplotlib import colors
import ipywidgets as widgets # ใช้สำหรับการทำ interactive display
num_points = 50 # # จำนวนจุดข้อมูล
x = np.linspace(-4, 4, num_points)
y = 1
# นำเอาค่า x มาใส่ใน column แรกของ data matrix และ ค่า y มาใส่ใน column ที่สอง
data = np.zeros((num_points, 2))
data[:, 0] = x
data[:, 1] = y
# เตรียมแสดงผล
x_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ x สำหรับแสดงผล
y_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ y สำหรับแสดงผล
plt.figure(figsize=(6, 6))
# แสดงรูปข้อมูลเริ่มต้น
plt.scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
plt.scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
plt.plot([0, 0], y_disp, c="grey") # Plot แกน y
plt.plot(x_disp, [0, 0], c="grey") # Plot แกน x
plt.xlabel("x")
plt.ylabel("y")
plt.title("Data with two classes")
plt.show()
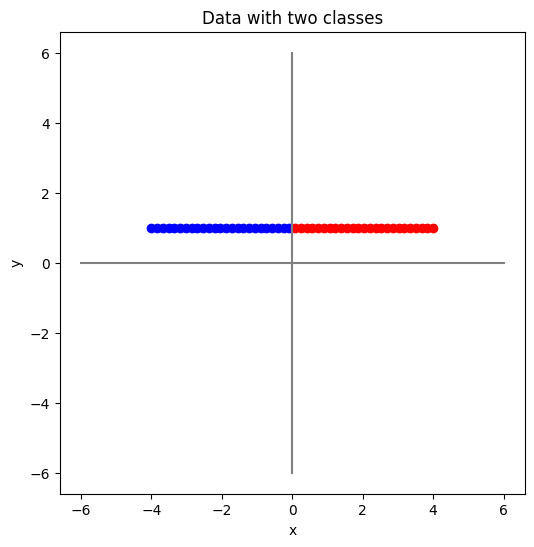
ถ้าหากเราต้องการแก้โจทย์ two-class classification หรือ แบ่งจุดข้อมูลที่เรามีออกเป็น 2 ประเภท (ประเภทน้ำเงิน และ ประเภทสีแดง) โดยที่เราใช้ค่า \(x\) เป็น feature แรก และใช้ค่า \(y\) เป็น feature ที่สอง เราสามารถใช้แกน \(y\) (สมการคือ \( x=0\)) แบ่งข้อมูลทั้ง 2 ประเภทออกจากกันได้เลย โดยเราจะตอบว่าจุดข้อมูลนั้นเป็น
class 1 (ประเภทที่ 1) ถ้าหากจุดนั้นมีค่า \(x\) น้อยกว่า \(0\) หรือถ้าดูจากภาพก็คือจุดนั้นอยู่ทางซ้ายของแกน \(y\)
class 2 (ประเภทที่ 2) ถ้าหากจุดนั้นมีค่า \(x\) มากกว่า \(0\) หรือถ้าดูจากภาพก็คือจุดนั้นอยู่ทางขวาของแกน \(y\)
จะเห็นว่าเราสามารถแบ่งจุดข้อมูลสองกลุ่มนี้ได้อย่างง่ายดาย โดยการดูแค่ค่า \(x\) อย่างเดียว โดยที่ไม่ต้องสนใจค่า \(y\) ซึ่งแปลว่าเราจริง ๆ แล้ว เราสามารถลดข้อมูลมิติของข้อมูลจากสองมิติ (\(x\) หนึ่งมิติ และ \(y\) เป็นอีกมิติ) ให้เหลือแค่มิติเดียว (ค่า \(x\) เพียงอย่างเดียว) ก็ยังสามารถ classify จุดเหล่านี้ได้เหมือนเดิม ดังแสดงในภาพด้านล่าง
x_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ x สำหรับแสดงผล
y_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ y สำหรับแสดงผล
# สร้างจุด (x,y) จำนวนมาก สำหรับเอามาใช้แสดงผล classification ที่จุดต่าง ๆ โดยใช้สีน้ำเงินแดง class 1 และสีแดงแสดง class 2
xx, yy = np.meshgrid(np.linspace(x_disp[0], x_disp[1], 100), np.linspace(y_disp[0], y_disp[1], 100))
# เก็บข้อมูลว่าแต่ละจุดถูก classify เป็น class อะไรบ้าง โดยใช้เลข 0 สำหรับ class 1 และ 1 สำหรับ class 2
labels_predicted = (xx.ravel() > 0).reshape(xx.shape)
# Plot ข้อมูลในสองมิติ
plt.figure(figsize=(4, 4))
plt.scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1 ด้วยสีน้ำเงิน
plt.scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2 ด้วนสีแดง
plt.plot([0, 0], y_disp, c="grey") # Plot แกน y
plt.plot(x_disp, [0, 0], c="grey") # Plot แกน x
plt.pcolormesh(xx, yy, labels_predicted, cmap=colors.ListedColormap(["blue", "red"]), norm=colors.Normalize(0.0, 1.0), zorder=0, alpha=0.3) # Plot ผลจากทำนายจากข้อมูล xx และ yy
plt.xlabel("x")
plt.ylabel("y")
plt.xlim(x_disp)
plt.ylim(y_disp)
plt.title("Data with two classes in 2-dimensional space")
# Plot ข้อมูลที่ลดมิติมาแล้ว
plt.figure(figsize=(4, 0.5))
plt.scatter(data[data[:, 0] < 0, 0], np.zeros_like(data[data[:, 0] < 0, 0]), c='b') # Plot จุดข้อมูลที่เป็น class 1
plt.scatter(data[data[:, 0] > 0, 0], np.zeros_like(data[data[:, 0] > 0, 0]), c='r') # Plot จุดข้อมูลที่เป็น class 2
plt.plot([0, 0], y_disp, c="grey") # Plot แกน y
plt.plot(x_disp, [0, 0], c="grey") # Plot แกน x
plt.pcolormesh(xx, yy, labels_predicted, cmap=colors.ListedColormap(["blue", "red"]), norm=colors.Normalize(0.0, 1.0), zorder=0, alpha=0.3) # Plot ผลจากทำนายจากข้อมูล xx เพึยงอย่างเดียว
plt.xlim(x_disp)
plt.ylim(-0.5, 0.5)
plt.title("Data with two classes in 1-dimensional space")
plt.yticks([])
plt.show()
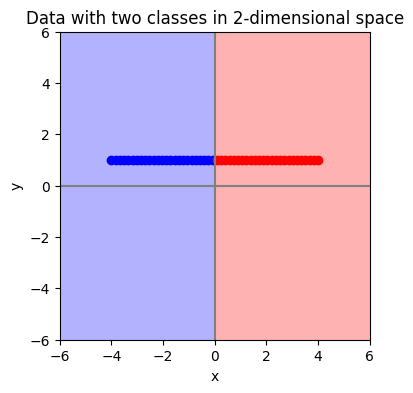
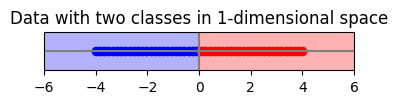
ตัวอย่างด้านบนแสดงให้เห็นว่าในบางชุดข้อมูล เราสามารถลดจำนวนมิติของข้อมูลได้ โดยที่ยังมีความสามารถในการทำ classification ได้เหมือนเดิม
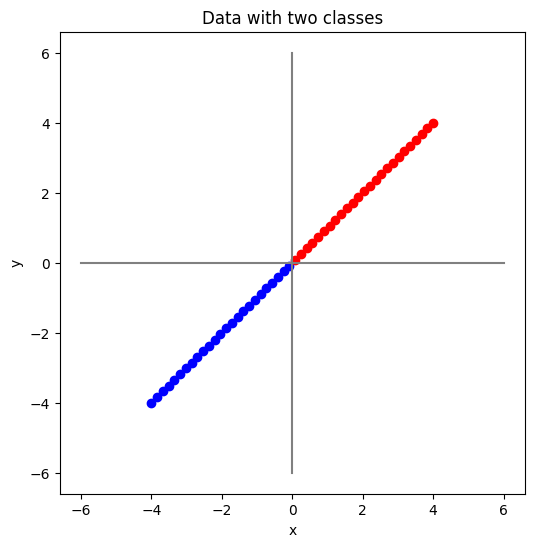
ตัวอย่างถัดมา สมมติว่าเรามีชุดข้อมูลชุดหนึ่ง ที่มีจุดข้อมูลอยู่ทั้งหมด 100 จุด แต่ละจุดข้อมูล \((x,y)\) เป็นข้อมูลใน space ที่มี 2 มิติ (ค่า \(x\) เป็นมิติแรก และค่า \(y\) เป็นมิติที่สอง) และในชุดข้อมูลนี้มีจุดอยู่ 2 ประเภท (2 classes)
class 1: \(y = x\) โดยที่ \( -4 ≤ x < 0 \)
class 2: \(y = x\) โดยที่ \( 0 < x ≤ 4 \)
ดังแสดงด้านล่าง
num_points = 50
x = np.linspace(-4, 4, num_points)
y = x
data = np.zeros((num_points, 2))
data[:, 0] = x
data[:, 1] = y
# เตรียมแสดงผล
x_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ x สำหรับแสดงผล
y_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ y สำหรับแสดงผล
plt.figure(figsize=(6, 6))
# แสดงรูปข้อมูลเริ่มต้น
plt.scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
plt.scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
plt.plot([0, 0], y_disp, c="grey") # Plot แกน y
plt.plot(x_disp, [0, 0], c="grey") # Plot แกน x
plt.xlabel("x")
plt.ylabel("y")
plt.title("Data with two classes")
plt.show()
จะเห็นว่าถ้าเรานำเอาข้อมูลด้านบนแต่ละจุดมาหมุนตามเข็มนาฬิกาไป \(45\) องศา โดยมีจุด \((0,0)\) เป็นจุดหมุน เราจะสามารถแปลงโจทย์ข้อนี้ให้กลายเป็นโจทย์ที่มีหน้าตาคล้ายกับข้อมูลในตัวอย่างก่อนหน้า
การหมุนจุดข้อมูลทวนเข็มนาฬิกาไป \(\theta\) องศาโดยมีจุด \((0,0)\) เป็นจุดหมุน สามารถอธิบายได้ด้วย rotation matrix
หากเรา represent พิกัด \((x,y)\) ด้วย vector
เราจะสามารถหมุนจุดข้อมูลนั้นตามเข็มนาฬิกา 45 องศา ด้วยการใช้ \(R(-45°)\)
เกิดเป็นพิกัด \((x',y')\)
ก่อนอื่นเรามาลองเล่นดูใน widget นี้ว่าเมื่อเปลี่ยน องศา แล้วข้อมูลจะเปลี่ยนไปอย่างไรบ้าง
Show code cell source
from IPython.core.display import HTML
HTML("""
<!DOCTYPE html>
<html>
<head>
<style>
canvas {
border: 1px solid black;
}
</style>
</head>
<body>
<input type="range" id="angleSlider" min="-180" max="180" value="0" step="1">
<div id="angleValue"></div>
<div id="transformationMatrix"></div>
<canvas id="canvas"></canvas>
<script>
// Generate x and y data points from Python code
const numPoints = 50;
const x = [-2.8284271247461903,-2.7129811169126663,-2.5975351161502105,-2.4820891083166865,-2.3666431075542302,-2.2511970997207067,-2.1357510918871827,-2.020305091124727,-1.9048590832912027,-1.789413075457679,-1.6739670746952229,-1.5585210668616991,-1.4430750660992433,-1.3276290582657193,-1.2121830504321953,-1.0967370496697393,-0.9812910418362154,-0.8658450410737594,-0.7503990332402356,-0.6349530254067116,-0.5195070246442557,-0.4040610168107318,-0.2886150160482758,-0.17316900821475187,-0.057723000381228025,0.057723000381228025,0.17316900821475187,0.2886150160482758,0.4040610168107318,0.5195070246442557,0.6349530254067116,0.7503990332402356,0.8658450410737594,0.9812910418362154,1.0967370496697393,1.2121830504321953,1.3276290582657193,1.4430750660992433,1.5585210668616991,1.6739670746952229,1.789413075457679,1.9048590832912027,2.020305091124727,2.1357510918871827,2.2511970997207067,2.3666431075542302,2.4820891083166865,2.5975351161502105,2.7129811169126663,2.8284271247461903];
const y = [-2.82842712474619,-2.7129811169126663,-2.59753511615021,-2.482089108316686,-2.3666431075542302,-2.2511970997207063,-2.1357510918871827,-2.0203050911247264,-1.9048590832912025,-1.7894130754576787,-1.6739670746952227,-1.558521066861699,-1.4430750660992429,-1.327629058265719,-1.212183050432195,-1.096737049669739,-0.9812910418362152,-0.8658450410737593,-0.7503990332402355,-0.6349530254067116,-0.5195070246442556,-0.40406101681073175,-0.2886150160482757,-0.17316900821475184,-0.05772300038122801,0.05772300038122801,0.17316900821475184,0.2886150160482757,0.40406101681073175,0.5195070246442556,0.6349530254067116,0.7503990332402355,0.8658450410737593,0.9812910418362152,1.096737049669739,1.212183050432195,1.327629058265719,1.4430750660992429,1.558521066861699,1.6739670746952227,1.7894130754576787,1.9048590832912025,2.0203050911247264,2.1357510918871827,2.2511970997207063,2.3666431075542302,2.482089108316686,2.59753511615021,2.7129811169126663,2.82842712474619];
// Combine x and y data into points array
const points = x.map((xVal, index) => ({
x: xVal * 50, // Scale x values to fit canvas
y: y[index] * 50, // Scale y values to fit canvas
original: true // Flag to indicate original points
}));
// Get the angle slider element
const angleSlider = document.getElementById('angleSlider');
// Get the value display elements
const angleValue = document.getElementById('angleValue');
const transformationMatrix = document.getElementById('transformationMatrix');
// Get the canvas element
const canvas = document.getElementById('canvas');
const context = canvas.getContext('2d');
// Function to update the rotation based on the slider value
function updateRotation() {
// Angle in degrees
const theta = angleSlider.value;
// Convert angle to radians
const thetaRad = (theta * Math.PI) / 180;
// Rotation matrix
const cosTheta = Math.cos(thetaRad);
const sinTheta = Math.sin(thetaRad);
const rotationMatrix = [
cosTheta, -sinTheta,
sinTheta, cosTheta
];
// Apply rotation transformation to each point
const rotatedPoints = points.map(point => ({
x: (point.x * rotationMatrix[0]) + (point.y * rotationMatrix[1]),
y: (point.x * rotationMatrix[2]) + (point.y * rotationMatrix[3]),
original: point.original
}));
// Find the maximum distance between the points
const distances = rotatedPoints.map(point => Math.sqrt(point.x ** 2 + point.y ** 2));
const maxDistance = Math.max(...distances);
// Calculate the canvas dimensions based on the maximum distance
const canvasSize = 2 * maxDistance + 20; // Add some padding
// Update canvas dimensions
canvas.width = canvasSize;
canvas.height = canvasSize;
// Calculate the center of the canvas
const centerX = canvas.width / 2;
const centerY = canvas.height / 2;
// Adjust the points to be relative to the center
const adjustedPoints = rotatedPoints.map(point => ({
x: centerX + point.x,
y: centerY - point.y, // Subtract to invert the y-axis
original: false
}));
const adjustedOriginalPoints = points.map(point => ({
x: centerX + point.x,
y: centerY - point.y, // Subtract to invert the y-axis
original: true
}));
// Clear canvas
context.clearRect(0, 0, canvas.width, canvas.height);
// Draw axes
context.beginPath();
context.moveTo(centerX, 0);
context.lineTo(centerX, canvas.height);
context.moveTo(0, centerY);
context.lineTo(canvas.width, centerY);
context.strokeStyle = 'gray';
context.stroke();
// Draw points
adjustedOriginalPoints.forEach((point, i) => {
let alpha = 0.1;
if (i < numPoints/2) {
context.fillStyle = `rgba(0, 0, 255, ${alpha})`; // First half of rotated points with blue color
} else {
context.fillStyle = `rgba(255, 0, 0, ${alpha})`; // Second half of rotated points with red color
}
context.beginPath();
context.arc(point.x, point.y, 4, 0, 2 * Math.PI);
context.fill();
});
adjustedPoints.forEach((point, i) => {
let alpha = 1;
if (i < numPoints/2) {
context.fillStyle = `rgba(0, 0, 255, ${alpha})`; // First half of rotated points with blue color
} else {
context.fillStyle = `rgba(255, 0, 0, ${alpha})`; // Second half of rotated points with red color
}
context.beginPath();
context.arc(point.x, point.y, 4, 0, 2 * Math.PI);
context.fill();
});
// Update angle value display
angleValue.textContent = `Angle: ${theta}°`;
// Update transformation matrix display
transformationMatrix.innerHTML = `
<table>
<tr>
<td>${rotationMatrix[0].toFixed(2)}</td>
<td>${rotationMatrix[1].toFixed(2)}</td>
</tr>
<tr>
<td>${rotationMatrix[2].toFixed(2)}</td>
<td>${rotationMatrix[3].toFixed(2)}</td>
</tr>
</table>
`;
}
// Add event listener to the angle slider
angleSlider.addEventListener('input', updateRotation);
// Initial rotation update
updateRotation();
</script>
</body>
</html>
""")
ตอนนี้เรามาลองหมุนข้อมูลกันโดยใช้ code ใน cell ถัดมากันดีกว่า
def rotate_counterclockwise(data, degree):
# สร้าง rotation matrix R ที่ทำหน้าที่ใช้หมุนพิกัดทวนเข็มนาฬิกา
R = np.array([[np.cos(degree), -np.sin(degree)],
[np.sin(degree), np.cos(degree)]])
return np.transpose(np.matmul(R, np.transpose(data)))
@widgets.interact(angle_counter_clock_degree=widgets.IntSlider(0, min=-180, max=180, description='Angle (deg)'),
show_original=widgets.Checkbox(True, description='Show original data'))
def plot_rotated_results(angle_counter_clock_degree, show_original):
# ทำการหมุนข้อมูล
data_rot = rotate_counterclockwise(data, angle_counter_clock_degree*(np.pi/180))
# สร้าง figure
fig, ax = plt.subplots(figsize=(6,6))
# Plot ข้อมูล x, y ที่มีอยู่ด้วยสีน้ำเงิน
ax.scatter(data_rot[data[:, 0] < 0, 0], data_rot[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax.scatter(data_rot[data[:, 0] > 0, 0], data_rot[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax.plot([0, 0], [-6.0, 6.0], c="m", alpha=0.5) # Plot แกน y ที่ถูกหมุน
ax.plot([-6.0, 6.0], [0, 0], c="m", alpha=0.5) # Plot แกน x ที่ถูกหมุน
if show_original:
ax.scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b', alpha=0.1) # Plot จุดข้อมูลที่เป็น class 1
ax.scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r', alpha=0.1) # Plot จุดข้อมูลที่เป็น class 2
ax.set_title(f"Data rotated by {angle_counter_clock_degree} degrees (counter-clockwise centered at (0,0))")
plt.show()
เรามาลองดูว่า ถ้าหมุนจุดข้อมูลเหล่านี้ตามเข็มนาฬิกาไป 45 องศา โดยมีจุดหมุนคือ \((0,0)\) ผลจะเป็นอย่างไร
# ใช้ rotation matrix คำนวณพิกัดใหม่ของจุดทั้งหมด
data_rot45 = rotate_counterclockwise(data, -np.pi/4)
# เตรียมแสดงผล
x_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ x สำหรับแสดงผล
y_disp = [-6.0, 6.0] # ค่าต่ำสูงและสูงสุดของ y สำหรับแสดงผล
fig, ax = plt.subplots(1, 2, figsize=(12, 6))
# แสดงรูปข้อมูลเริ่มต้น
ax[0].scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax[0].scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax[0].plot([0, 0], y_disp, c="grey") # Plot แกน y
ax[0].plot(x_disp, [0, 0], c="grey") # Plot แกน x
ax[0].set(xlabel="x", ylabel="y")
ax[0].set_title("Data with two classes")
# แสดงรูปหลังหมุนข้อมูลตามเข็มนาฬิกาไป 45 องศา
ax[1].scatter(data_rot45[data[:, 0] < 0, 0], data_rot45[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax[1].scatter(data_rot45[data[:, 0] > 0, 0], data_rot45[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax[1].plot([0, 0], y_disp, c="grey") # Plot แกน y
ax[1].plot(x_disp, [0, 0], c="grey") # Plot แกน x
ax[1].set(xlabel="Rotated x", ylabel="Rotated y")
ax[1].set_title("Rotated data (45 degrees clockwise)")
plt.setp(ax, xlim=x_disp, ylim=y_disp)
# Plot ข้อมูลที่ลดมิติมาแล้ว
plt.figure(figsize=(4, 0.5))
plt.scatter(data_rot45[data[:, 0] < 0, 0], np.zeros_like(data_rot45[data[:, 0] < 0, 0]), c='b') # Plot จุดข้อมูลที่เป็น class 1
plt.scatter(data_rot45[data[:, 0] > 0, 0], np.zeros_like(data_rot45[data[:, 0] > 0, 0]), c='r') # Plot จุดข้อมูลที่เป็น class 2
plt.plot([0, 0], y_disp, c="grey") # Plot แกน y
plt.plot(x_disp, [0, 0], c="grey") # Plot แกน x
plt.xlim(x_disp)
plt.ylim(-0.5, 0.5)
plt.title("Rotated data with two classes in 1-dimensional space")
plt.yticks([])
plt.show()
plt.show()
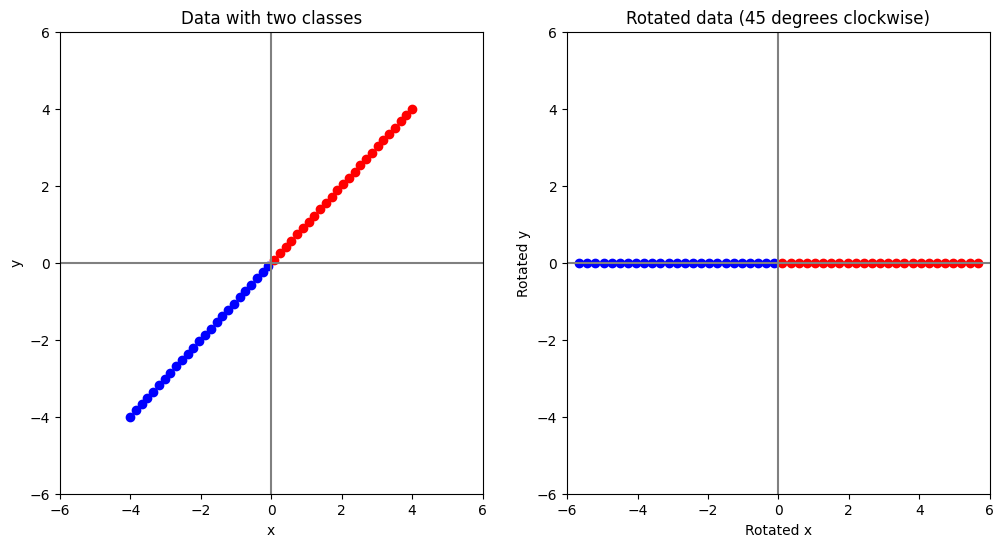
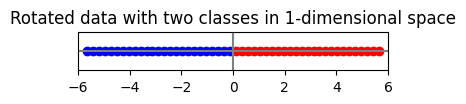
มีข้อสังเกตดังนี้
ข้อมูลเริ่มต้นอยู่ใน space ขนาด 2 มิติ โดยมีลักษณะเป็นเส้นตรงที่ทำมุม \(45\) องศากับแกน \(x\)
ถ้าหากเราหมุนจุดข้อมูลเหล่านั้นตามเข็มนาฬิกาไป \(45\) องศา เราจะเห็นข้อมูลจัดเรียงกันอยู่บนแกน \(x\) โดยที่ค่าใน แกน \(y\) ทุกตัวเป็น \(0\)
ถ้าหากเราต้องการจะ classify ข้อมูลนี้ เราสามารถทำได้โดยการดูแค่ค่าในแกน \(x\) (ไม่ต้องดูแกน \(y\) เลย) แสดงว่าเราสามารถลดจำนวนมิติของข้อมูลให้เหลือ \(1\) มิติได้ โดยที่ยังมีความสามารถในการทำ classification ได้เหมือนเดิม
จะเห็นได้ว่าในหลาย ๆ ครั้ง เราสามารถลดจำนวนมิติได้ ซึ่งในตัวอย่างเหล่านี้เราแค่ใช้การ transform จุดข้อมูลอย่างง่าย เช่น การหมุน ก็ส่งผลให้ข้อมูลมาอยู่ในรูปแบบที่เราสามารถกำจัดแกน \(y\) ได้เลย ส่งผลให้จำนวนมิติลดลงจาก 2 มิติ ไปเป็น 1 มิติ และเรายังพบว่าเราสามารถนำเอาข้อมูลใน 1 มิตินี้ไปใช้งานต่อได้ เช่น เรายังสามารถนำเอาไปใช้เป็น feature ในการ classify ได้เหมือนเดิม
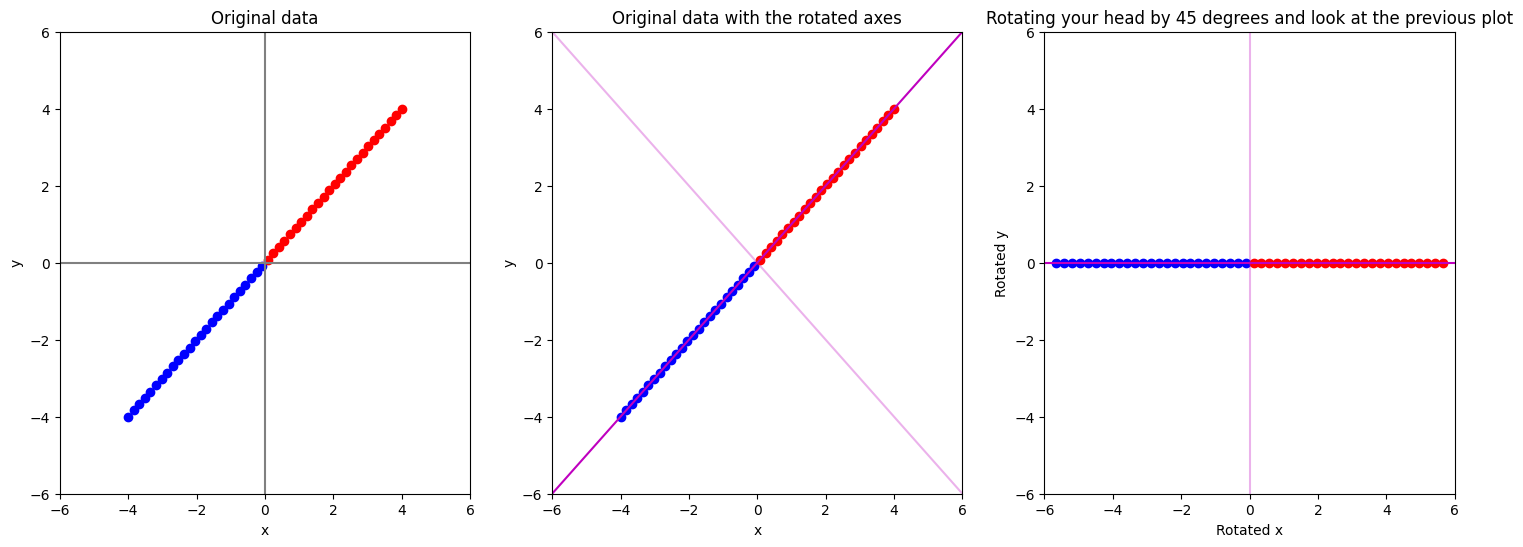
ข้อสังเกต ในตัวอย่างล่าสุด เราหมุนจุดข้อมูลไป \(45\) องศาแบบตามเข็มนาฬิกา โดยที่ไม่ขยับแกน \(x\) และ แกน \(y\) เลย ซึ่งการทำแบบนี้ ในอีกมุมมองนึง ก็เหมือนกับการหมุนแกน \(x\) และ แกน \(y\) ไป \(45\) องศาแบบทวนเข็มนาฬิกา โดยที่ไม่ขยับจุดข้อมูล ซึ่งเราจะใช้สีชมพูเข้มแสดงแกน \(x\) ที่ถูกหมุน และ สีชมพูอ่อนแสดงแกน \(y\) ที่ถูกหมุน (แล้วเอียงศีรษะไป \(45\) องศาทวนเข็มนาฬิกาขณะดูภาพ) ดังแสดงด้วยตัวอย่าง code ใน cell ถัดมา
fig, ax = plt.subplots(1, 2, figsize=(9.5, 6))
# แสดงรูปข้อมูลเริ่มต้น
ax[0].scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax[0].scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax[0].plot([0, 0], y_disp, c="grey") # Plot แกน y
ax[0].plot(x_disp, [0, 0], c="grey") # Plot แกน x
ax[0].set(xlabel="x", ylabel="y")
ax[0].set_title("Original data")
# แสดงรูปหลังหมุนข้อมูลตามเข็มนาฬิกาไป 45 องศา
ax[1].scatter(data_rot45[data[:, 0] < 0, 0], data_rot45[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax[1].scatter(data_rot45[data[:, 0] > 0, 0], data_rot45[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax[1].plot([0, 0], y_disp, c="grey") # Plot แกน y
ax[1].plot(x_disp, [0, 0], c="grey") # Plot แกน x
ax[1].set(xlabel="Rotated x", ylabel="Rotated y")
ax[1].set_title("Rotated data (45 degrees clockwise)")
fig, ax = plt.subplots(1, 3, figsize=(18, 6))
# แสดงรูปข้อมูลเริ่มต้น
ax[0].scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax[0].scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax[0].plot([0, 0], y_disp, c="grey") # Plot แกน y
ax[0].plot(x_disp, [0, 0], c="grey") # Plot แกน x
ax[0].set(xlabel="x", ylabel="y")
ax[0].set_title("Original data")
# แสดงรูปข้อมูลที่มีการหมุนแกนทวนเข็มนาฬิการไป 45 องศา
# แสดงรูปข้อมูลเริ่มต้นโดยมี principal component ทั้ง 2 อันแสดงอยู่ด้วย
ax[1].scatter(data[data[:, 0] < 0, 0], data[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax[1].scatter(data[data[:, 0] > 0, 0], data[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax[1].plot(x_disp, [x_disp[0], x_disp[1]], c="m", alpha=1) # แสดง pc1 โดยใช้สมการ y = x
ax[1].plot(x_disp, [-x_disp[0], -x_disp[1]], c="m", alpha=0.3) # แสดง pc2 โดยใช้สมการ y = -x
ax[1].set(xlabel='x', ylabel='y')
ax[1].set_title("Original data with the rotated axes")
# แสดงข้อมูลที่หมุนแกนและเอียงศีรษะดู
ax[2].scatter(data_rot45[data[:, 0] < 0, 0], data_rot45[data[:, 0] < 0, 1], c='b') # Plot จุดข้อมูลที่เป็น class 1
ax[2].scatter(data_rot45[data[:, 0] > 0, 0], data_rot45[data[:, 0] > 0, 1], c='r') # Plot จุดข้อมูลที่เป็น class 2
ax[2].plot(x_disp, [0, 0], c="m", alpha=1)
ax[2].plot([0, 0], y_disp, c="m", alpha=0.3)
ax[2].set(xlabel="Rotated x", ylabel="Rotated y")
ax[2].set_title("Rotating your head by 45 degrees and look at the previous plot")
plt.setp(ax, xlim=x_disp, ylim=y_disp)
plt.show()
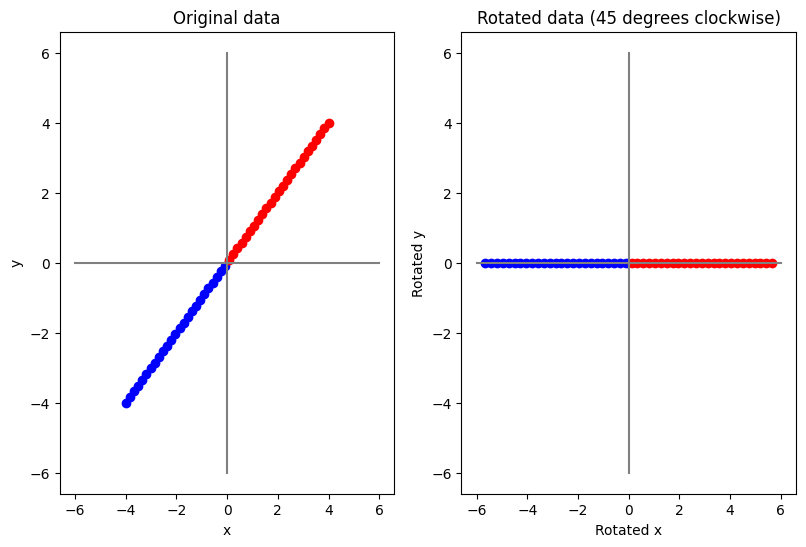
ในสถานการณ์การทำงานจริง เรามักเจอข้อมูลที่มีความซับซ้อนมาก เช่น ข้อมูลที่อยู่ใน space ที่มีจำนวนมิติสูงมาก เราอาจจะไม่สามารถใช้การ transform แบบง่าย ๆ ที่เราใช้ในตัวอย่างนี้ จึงมีเทคนิคมากมายถูกคิดค้นขึ้นเพื่อใช้ช่วยลดมิติของข้อมูลของเราได้อย่างมีประสิทธิภาพ
ผู้จัดเตรียม code ใน tutorial: ดร. อิทธิ ฉัตรนันทเวช และ ดร. สุรัฐ ธีรพิทยานนท์